Raoult’s Law and applications 2
Table of Contents
Vapor pressure of the liquid-liquid solution
Raoult’s law and applications 2 are based on the vapor pressure of a solution or liquid. Raoult’s law explains how the vapor pressure of liquid-liquid miscible solution varies with changing the mole fraction of the components present in the solution.
To understand Raoult’s law following definitions are necessary
Vapor Pressure
It is the pressure of vapors exerted over the liquid surface.
In a closed system when a liquid is kept evaporation would take place as a result of which some vapors would be collected, these vapors would exert pressure over the liquid surface.
The pressure exerted by the vapors on the liquid surface is termed vapor pressure.
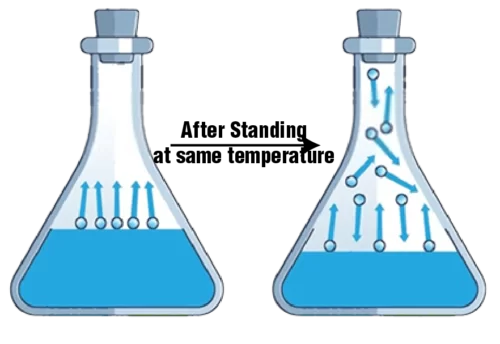
Vapor pressure is dependent on temperature as temperature increases the vapor pressure increases.
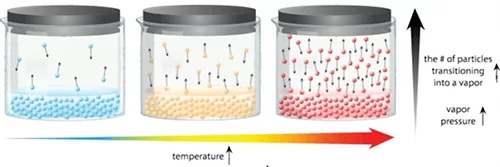
Boiling point
In Raoult’s law and applications 2, boiling point is a temperature at which the vapor pressure of the liquid is equal to external or atmospheric pressure.
The boiling point of water is 100o C at one atmospheric pressure or at sea level as pressure is increased the boiling point of water would also increase and vice versa if pressure is decreased then the boiling point decreases.
The cooking is prolonged when cooked in an open vessel at high altitudes because at high altitudes the pressure is less. Water boils at a lower temperature than its boiling point so cooking is prolonged.
Raoult’s law and applications
Raoult’s Law and applications 2 is a quantitative relationship between the vapor pressure of the liquid in a solution and the mole fraction of liquid in the solution.
It is defined as the total vapor pressure of the solution as a simple algebraic sum of partial pressures of all the components present in the solution.
For a binary solution A and B, the total vapor pressure can be written as
Ideal solution
According to Raoult’s Law and applications 2 Liquid-Liquid solutions can be classified into two types according to Raoult’s law
A solution is said to be ideal if it obeys two conditions:
Change in enthalpy for mixing (ΔH(mix)) should be equal to 0. This means when two liquids are mixed there should not be changing heat during mixing. Let us suppose benzene and toluene are mixed and both the liquids are at 25°C then after mixing if the temperature of the solution remains 25°C then the change in enthalpy for mixing would be zero
The change in volume for mixing (ΔV(mix)) should be equal to 0. This means when two liquids are mixed the total volume after mixing should be a simple algebraic sum of volumes of two liquids that are mixed. Suppose 50 mL of benzene is mixed with 75 mL of toluene and after mixing the volume of the solution is 125 mL then the change in volume for mixing would be zero.
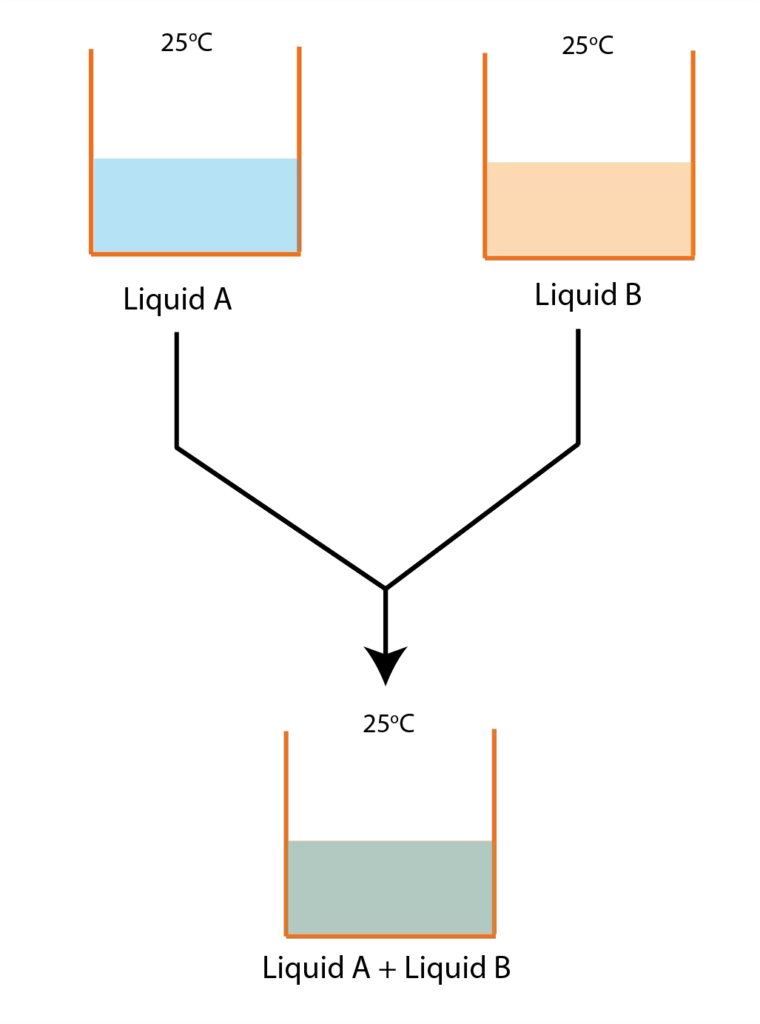
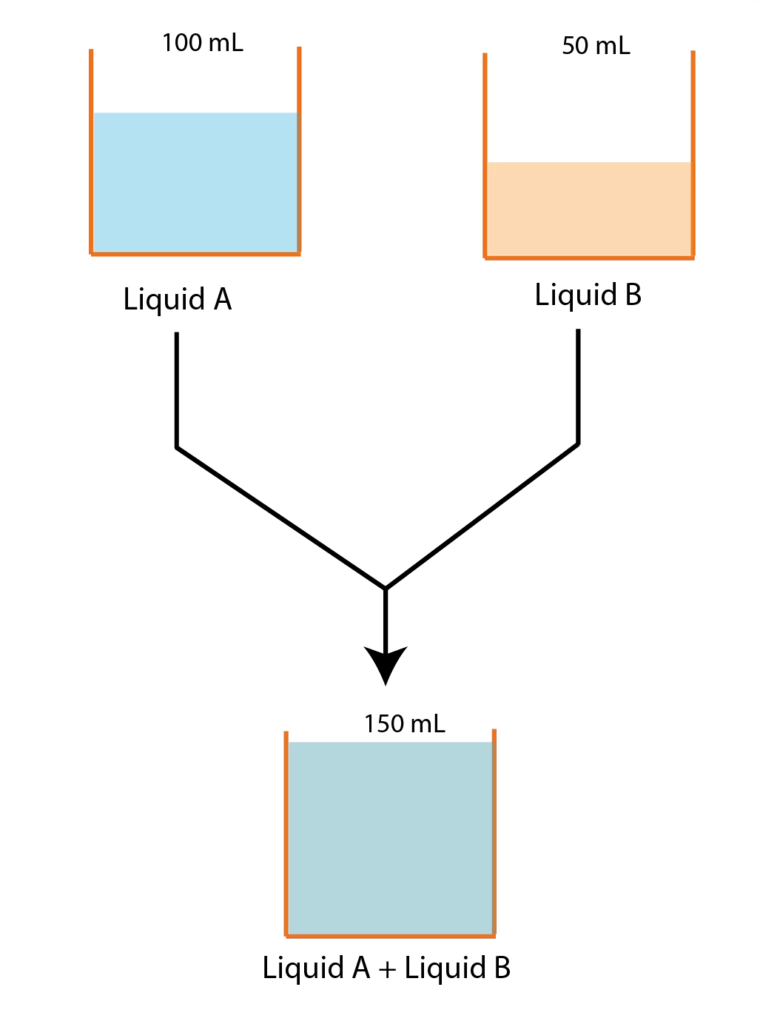
Graphical representation of Ideal Solution
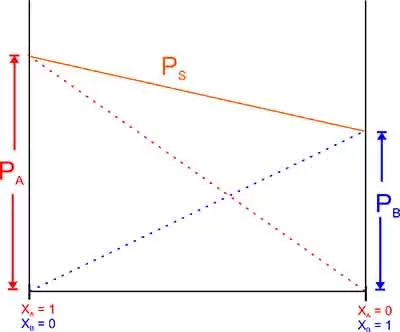
Raoult’s Law and its applications 2 has conditions for solution being Ideal
- ΔH mix. = Zero
- ΔV mix. = Zero
- Obey Raoult’s Law
In the above ideal solution explanation molecular interactions are not considered, so in solutions formed by liquids possess interactions and thus deviation is observed.
Two types for deviations are observed.
- Positive deviation form Raoult’s Law
- Negative deviation form Raoult’s Law
Positive Deviation
Raoult’s law and applications 2, Positive Deviations occur when the interactions between different molecules in the mixture are weaker than the interactions present in the pure components. This often leads to an increase in enthalpy, as energy is required to overcome these weaker attractions.
A classic example can be seen in mixtures of volatile liquids, such as ethanol and water, where the formation of hydrogen bonds between the molecules is not as strong as the hydrogen bonds in pure ethanol or pure water.
As a result, the vapor pressure of the mixture is higher than what would be expected for an ideal solution, leading to a greater volume change upon mixing.
This phenomenon is crucial for processes like distillation, where understanding these changes can optimize separation techniques.
Positive Deviation Characteristics
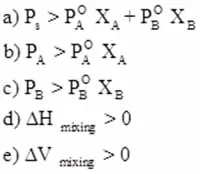
Solutions showing positive deviation from Raoult’s Law
- Acetone + Ethanol
- Acetone- Benzene
- Water + Methanol
- Water + Ethanol
- Carbon disulphide + acetone
Negative Deviation
Negative Deviations occur when the interactions between different molecules are stronger than those in the pure components. This typically results in a release of energy, leading to a decrease in enthalpy during the mixing process.
A prime example is the mixing of acetone and water, where strong hydrogen bonding occurs between the acetone and water molecules. This increased interaction reduces the overall vapor pressure of the mixture compared to the ideal prediction, indicating that the solution is more stable and compact.
The result is a contraction in volume upon mixing, which can have significant implications for industrial processes, such as chemical reactions where precise control of concentration and volume is necessary.
Negative Deviation Characteristics
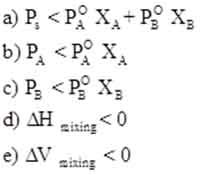
Solutions showing negative deviation from Raoult’s Law
- Acetone + Chloroform
- Acetone + Aniline
- Water + HCl
- Water + Nitric Acid
- Chloroform + Diethyl Ether
- Chloroform + Benzene
Azeotropes:
Raoult’s Law and its applications 2 can form Azeotropes. These are binary mixtures having same composition in liquid and vapor phase and boil at constant temperature. Liquids forming azeotrope cannot be separated by fractional distillation.
Types of azeotropes: There are two types of azeotropes namely,
- Minimum boiling azeotrope: The solutions which show a large positive deviation from Raoult’s law form minimum boiling azeotrope at a specific composition
- Maximum boiling azeotrope: The solutions that show large negative deviation from Raoult’s law form maximum boiling azeotrope at a specific composition.
Case Studies: Enthalpy and Volume Changes in Different Solutions
In the realm of thermodynamics and solution chemistry, understanding the intricacies of enthalpy and volume changes during mixing is crucial for predicting the behavior of various solutions. To illustrate these principles in action, let’s delve into a few compelling case studies that highlight the deviations in enthalpy and volume changes across different types of solutions.
Case Study 1: Salt in Water
When sodium chloride (NaCl) is dissolved in water, the process is endothermic, meaning it absorbs heat from the surroundings. This is observable in the slight drop in temperature of the solution as the salt is added. During this mixing, the volume of the solution may appear to increase marginally; however, the overall change can be deceptively small due to the ion-dipole interactions that occur between the water molecules and the dissociated ions.
This example illustrates how an endothermic reaction can lead to complex changes in both enthalpy and volume, challenging the assumption that dissolving a solid always results in a straightforward increase in solution volume.
Case Study 2: Acetic Acid and Water
Conversely, when acetic acid (CH₃COOH) is mixed with water, a fascinating exothermic reaction occurs. The strong hydrogen bonding between the acetic acid molecules and water leads to a significant release of heat. Interestingly, this process also results in a volume contraction, where the total volume of the solution decreases compared to the initial volumes of the individual components.
This case study highlights how the interactions between solute and solvent not only affect the thermal properties of the solution but also induce noteworthy changes in volume.
Case Study 3: Ethanol and Water
Another intriguing example can be found in the mixing of ethanol and water. When these two liquids are combined, they undergo a significant decrease in volume, a phenomenon often attributed to the ability of ethanol to fit into the spaces between water molecules. The mixing process is exothermic as well, albeit to a lesser extent compared to acetic acid.
This case serves as a reminder of the intricate relationships between molecular structure, mixing behavior, and thermodynamic properties.
Through these case studies, we gain invaluable insights into how enthalpy and volume changes during mixing can vary dramatically depending on the nature of the solute and solvent involved.
By examining these real-world examples, we can better appreciate the complex interactions at play within ideal solutions and enhance our understanding of solution chemistry as a whole.