Abnormal Molecular Mass
Abnormal Molecular Mass
Table of Contents
Introduction: Abnormal Molecular Mass
Understanding the intricacies of abnormal molecular mass in solution is crucial for CBSE students aiming to excel in their examinations.
As chemistry enthusiasts delve into the fascinating world of solutes and solvents, they often encounter the perplexing yet essential concept of how adding solute to a solvent can led to deviations in expected molecular mass.
Whether you’re preparing for your board exams or simply keen on mastering this pivotal topic, our blog post will guide you through the key principles and practical applications surrounding this phenomenon.
With insightful explanations, illustrative examples, and effective study tips from Myetutors, you’ll be well-equipped to navigate the challenges of this subject and achieve academic success.
Join us as we explore the art and science behind abnormal molecular mass, ensuring you’re ready to tackle any questions that come your way!
What is Abnormal Molecular Mass
Abnormal molecular mass refers to the phenomenon observed in solutions where the calculated molecular mass of a solute differs significantly from its expected value.
This discrepancy arises when a solute is dissolved in a solvent, and it impacts the colligative properties of the solution, leading to unusual results in experiments, particularly in the context of CBSE examinations.
In essence, the molecular mass of a substance is typically determined based on its composition and structure under ideal conditions. However, when a solute is introduced to a solvent, especially in high concentrations or in the presence of strong interactions, various factors can contribute to this abnormality. These include ionization or dissociation of the solute in solution, the formation of complex ions, or the presence of impurities.
For instance, when an ionic compound like sodium chloride (NaCl) dissolves in water, it separates into sodium (Na⁺) and chloride (Cl⁻) ions. The effective number of particles in the solution is greater than one for each formula unit of the solute, which leads to a lower-than-expected molecular mass when calculating based on molality or molarity.
Understanding abnormal molecular mass is crucial for tasks such as calculating the molecular weight of a compound using freezing point depression or boiling point elevation methods.
These concepts often appear in CBSE examinations, highlighting the importance of grasping the intricacies of solutions and their behaviors. Consequently, students preparing for these assessments should not only memorize definitions but also actively engage with problems that illustrate these concepts in practice, exemplifying the importance of myetutors as an educational resource for clarification and practice.
Vant Hoff's Factor and Abnormal Molecular mMass
Vant Hoff’s Factor Understanding colligative properties is crucial for mastering solutions, and one of the key concepts that CBSE students must grasp is Vant Hoff’s factor
(i). This factor plays a significant role in calculating the effects of solute particles on the physical properties of a solvent, particularly when dealing with abnormal molecular masses.
Simply put, Vant Hoff’s factor quantifies how a solute affects the colligative properties—such as boiling point elevation, freezing point depression, and osmotic pressure—based on the number of particles it dissociates into when dissolved.
For instance, when you dissolve a solute in a solvent, the extent to which it alters the properties of the solution depends not just on the amount of solute, but on how many particles are produced from that solute.
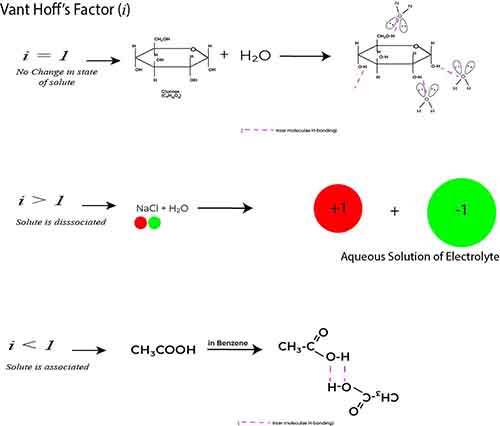
A non-electrolyte, like glucose, doesn’t ionize in solution and thus has a Vant Hoff’s factor of 1.
However, ionic compounds, such as sodium chloride (NaCl), dissociate into two ions—sodium (Na⁺) and chloride (Cl⁻)—resulting in a Vant Hoff’s factor of 2.
In the context of abnormal molecular mass, the Vant Hoff’s factor becomes a critical tool. Sometimes, the measured molecular mass of a solute in a solution appears to deviate from its expected value due to incomplete dissociation or association of solute particles.
This is where Vant Hoff’s factor helps clarify the situation. When calculating the molar mass of a solute using colligative properties, correcting for the appropriate Vant Hoff’s factor allows students to obtain more accurate results and avoid pitfalls in their calculations.
It’s essential for CBSE students to practice applying Vant Hoff’s factor in various scenarios, as understanding its implications will not only aid in solving examination problems but also deepen their appreciation of how solutes behave in different states.
By mastering this concept, students can confidently tackle questions and perform experiments related to solutions, reinforcing their foundational knowledge in chemistry.
Vant Hoff's Factor for non-Electrolyte solute
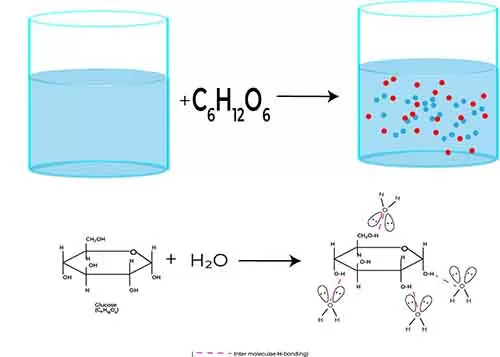
Vant Hoff’s Factor for Non-Electrolytes Understanding the concept of Van’t Hoff’s factor (i) is crucial for grasping the behavior of solutions in your CBSE examinations, particularly when discussing abnormal molecular masses. For non-electrolytes, which are substances that do not dissociate into ions when dissolved in a solvent, but these compounds interact with solvents molecules for dissolution.
The Van’t Hoff factor is straightforward and usually equals one (i = 1). This consistency simplifies calculations related to colligative properties like boiling point elevation and freezing point depression, where these properties depend solely on the number of solute particles in solution.
When you add a non-electrolyte solute, such as sugar or urea, to a solvent, the solute molecules remain intact. This means that regardless of how many solute molecules you add, they contribute equally to the colligative effects because they do not separate into different particles. Hence, the molecular mass of the solution appears altered due to the presence of the solute, leading to observable changes in its physical properties.
Vant Hoff's Factor for Dissociation of Solute
In the world of solutions and colligative properties, understanding Van ‘t Hoff’s factor (i) for electrolytes is crucial, especially when preparing for CBSE examinations.
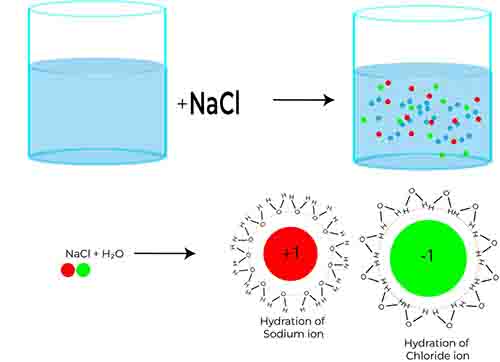
Van ‘t Hoff’s factor is a measure of the number of particles a solute generates in solution. For electrolytes, which are substances that dissociate into ions when dissolved in a solvent, this factor becomes even more critical because it directly influences the behavior of the solution.
When an electrolyte, such as sodium chloride (NaCl), dissolves in water, it ionizes into its constituent ions: sodium (Na⁺) and chloride (Cl⁻). This dissociation means that one formula unit of NaCl produces two particles in solution. Consequently, for this particular electrolyte, the Van ‘t Hoff’s factor i maximum would be 2. This concept is vital, as it affects key colligative properties, including boiling point elevation, freezing point depression, and osmotic pressure—properties that are often tested in examinations.
However, not all electrolytes behave ideally. For example, a strong electrolyte like potassium sulfate (K₂SO₄) dissociates into three ions (2 K⁺ and 1 SO₄²⁻), giving it a Van ‘t Hoff’s factor maximum of 3.
Conversely, weak electrolytes like acetic acid (CH₃COOH) do not fully dissociate; hence, their Van ‘t Hoff’s factor is less than their stoichiometric value.
Understanding these nuances will aid students in calculating abnormal molecular masses in solutions accurately. In practical scenarios, applying Van ‘t Hoff’s factor allows students to anticipate how solutes will behave in various solvent conditions, deepening their understanding of solution chemistry
Vant Hoff's factor for Association of Solute
Vant Hoff’s factor (i) quantifies the effect of solute particles on the physical properties of a solution. For non-electrolytes, the factor is typically equal to one, since they do not dissociate into ions. However, when a solute associates—meaning multiple solute molecules bond together rather than existing as free particles—the Vant Hoff’s factor deviates from one.
This deviation is significant, as it directly influences the calculated molecular mass of the solute in a solution.
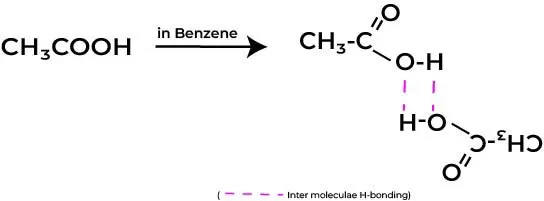
For example, if a solute like acetic acid (CH₃COOH) is added to a solvent (non-polar), it may partially associate to form dimers in the solution. In such cases, instead of acting as two separate particles contributing to colligative properties, the associated molecules may behave as one, leading to an effective decrease in the expected number of solute particles.
As a result, the Vant Hoff’s factor could be represented as i < 1, showcasing this association. Recognizing this phenomenon is essential for accurately determining the abnormal molecular mass of a solute in solution.
By employing the Van ‘t Hoff equation, students can approach quantitative problems, yielding insights into the molecular behavior of solutions.
For your CBSE examinations, be sure to familiarize yourself with how association impacts colligative properties, as well as the practical implications of determining the Vant Hoff’s factor in various experimental scenarios. Understanding these principles will not only enhance your comprehension of solutions but will also give you a firm foundation in tackling related exam questions with confidence.
